Условие задачи
Найдите ошибку в рассуждении: «Определим, при каких значениях параметра w корни квадратного уравнения
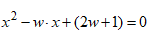
лежат на числовой прямой правее единицы. Условие расположения корней можно записать в виде системы неравенств:
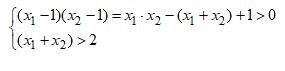
Первое неравенство утверждает, что корни находятся на оси абсцисс по одну сторону от 1, выполнение второго неравенства исключает ситуацию «левее единицы», которому соответствует произведение отрицательных величин в первом неравенстве.
Согласно формулам Виета для корней приведенного квадратного уравнения, выполняются соотношения
.
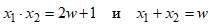Подставив в указанную выше систему неравенств, которые задают расположение корней относительно единицы, получим систему
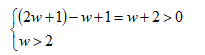
Значение параметра w=4 удовлетворяет полученным условиям, следовательно, оба корня уравнения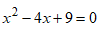 
расположены на числовой оси правее единицы».
Ответ
Ошибка в рассуждениях выделена красным шрифтом. Данные соотношения-то верны, но ЕСЛИ корни существуют! Нет, эти соотношения будут верны, даже если действительных корней нет (а оба корня- мнимые). Но делать отсюда какой-то вывод ПРО ДЕЙСТВИТЕЛЬНЫЕ корни (зелёным шрифтом) ну никак нельзя! Так как ещё НЕ доказано, что такие (действительные) корни есть!
В принципе - задача решена. Так как требовалось только НАЙТИ ошибку в рассуждениях, а не решить данный пример правильно.
Но всё-таки найдём именно такие значения параметра w, при которых оба корня будут правее единицы.
Во первых: уравнение ДОЛЖНО име...
