Найдите решение дифференциального уравнения. y^''+6y^'+13y=e^(-3x) cos4x k2+6k+13=0 ⇒ k1,2=-3±2i ⇒ y_оо=e^(-3x) (C_1 cos2x+C_2 sin2x ) y_чн=e^(-3x) (C_1 cos4x+C_2 sin4x );y^'=e^(-3x) ((-3C_1+4C_2 ) cos4x+(-4C_1-3C_2 ) sin4x );
«Найдите решение дифференциального уравнения. y^''+6y^'+13y=e^(-3x) cos4x k2+6k+13=0 ⇒ k1,2=-3±2i ⇒ y_оо=e^(-3x) (C_1 cos2x+C_2 sin2x ) y_чн=e^(-3x) (C_1 cos4x+C_2 sin4x );y^'=e^(-3x) ((-3C_1+4C_2 ) cos4x+(-4C_1-3C_2 ) sin4x );»
- Высшая математика
Условие:
Найдите решение дифференциального уравнения.
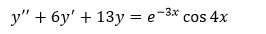
Решение:
k2 + 6k + 13 = 0 k1,2 = -3 2i yоо = e-3x (C1 cos2x + C2 sin2x )
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э