Условие задачи
Дана функция:
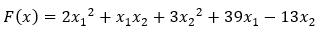
1) Найти экстремум и определить его тип (max или min) для заданной функции классическим методом, используя необходимые и достаточные условия существования экстремума.
2) Задать начальную точку и выполнить четыре шага градиентным методом с постоянным шагом
3) Задать начальную точку и выполнить три шага методом наискорейшего спуска.
4) Задать начальную точку и выполнить два шага методом Гаусса - Зейделя.
5) Задать начальную точку и выполнить 1 шаг методом Ньютона
6) Дать графическую иллюстрацию каждого метода на одном рисунке.
7) Выбрать одну и ту же начальную точку для каждого метода исходя из точного решения самостоятельно.
Ответ
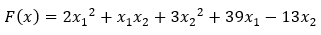
1) Найдем стационарные точки, в которых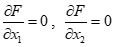 
, (необходимые условия экстремума).
