Условие:
Результаты измерений некоторой физической величины представлены в таблице:
1.1. Найти функцию распределения выборки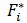 
и построить ее график.
1.2. Построить гистограмму относительных частот.
1.3. Найти числовые характеристики выборки: выборочное среднее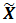 
и исправленную выборочную дисперсию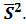 
1.4. Используя функцию Лапласа, построить доверительный интервал для математического ожидания, соответствующий доверительной вероятности 
1.5. С помощью критерия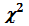 
(Пирсона) проверить гипотезу о нормальном распределении генеральной совокупности при уровне значимости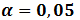 
Решение:
1. Эмпирическая функция распределения выборки.
Чтобы построить функцию распределения, необходимо определить середину каждого интервала и рассчитать относительные частоты и накопленные частости по формулам:
Середина интервала:
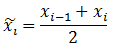
Относительные частоты: