Найти глоб макс фун зед равно икс минус 1 в 2 плюс игрек минус 3 в 3 множестве реш системы нер. икс плюс 2 игрек минус 14 меньше или равно 0, икс плюс игрек меньше или равно 9, 3 икс плюс игрек меньше или равно 21, икс и игрек больше или равно 0.
«Найти глоб макс фун зед равно икс минус 1 в 2 плюс игрек минус 3 в 3 множестве реш системы нер. икс плюс 2 игрек минус 14 меньше или равно 0, икс плюс игрек меньше или равно 9, 3 икс плюс игрек меньше или равно 21, икс и игрек больше или равно 0.»
- Высшая математика
Условие:
Найти глобальный максимум функции z = (x – 1)2 + (y – 3)3 множестве решений системы неравенств.
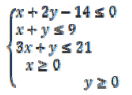
Решение:
Предположим, что мы начали с некоторого допустимого решения, определенного координатами точки К. Градиент или r1 является вектором, перпендикулярным касательной к линии уровня в точке К. Мы двигаемся из точкиК в направлении r1 до тех пор, пока не достигнем границы множества допустимых решений К1. Дальше двигаться мы не можем в направлении r2(r2 =, так как при этом мы выйдем из множества допустимых решений. Поэтому мы выбираем вектор r3, составляющий с вектором r2 наименьший угол по сравнению с любым другим вектором сначалом в точке К1 и лежащим в множестве допустимых решений. Таким образом, на...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э