Найти интеграл от функции комплексного переменного, используя основную теорему Коши о вычетах:
«Найти интеграл от функции комплексного переменного, используя основную теорему Коши о вычетах:»
- Высшая математика
Условие:
Найти интеграл от функции комплексного переменного, используя основную теорему Коши о вычетах:
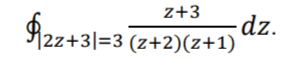
Решение:
1) Определим изолированные особые точки подинтегральной функции
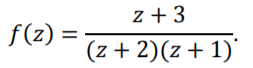
Особые точки: 𝑧 = 1, 𝑧 = 2.
2) Определим точки, лежащие внутри области интегрирования, изобразим область |2𝑧 + 3| = 3.
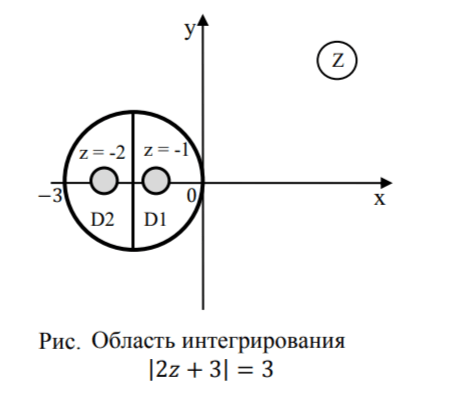
Обе особые точки 𝑧0 ...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э