1. Главная
  2. Библиотека
  3. Высшая математика
  4. Найти общее решение дифференциального уравнения: (1+x^2 ) y^''+2xy^'=x^3 y=1/4 ∫(x^4 dx)/(1+x^2 )+C_1 ∫dx/(1+x^2 )=1/4 ∫(x...

Найти общее решение дифференциального уравнения: (1+x^2 ) y^''+2xy^'=x^3 y=1/4 ∫(x^4 dx)/(1+x^2 )+C_1 ∫dx/(1+x^2 )=1/4 ∫(x^2-1+1/(x^2+1))dx+C_1 ∫dx/(1+x^2 )==1/12 x^3-1/4 x+1/4 arctg x+C_1 arctg x+C_2=1/12 x^3-1/4 x+C_3 arctg x+C_2

«Найти общее решение дифференциального уравнения: (1+x^2 ) y^''+2xy^'=x^3 y=1/4 ∫(x^4 dx)/(1+x^2 )+C_1 ∫dx/(1+x^2 )=1/4 ∫(x^2-1+1/(x^2+1))dx+C_1 ∫dx/(1+x^2 )==1/12 x^3-1/4 x+1/4 arctg x+C_1 arctg x+C_2=1/12 x^3-1/4 x+C_3 arctg x+C_2»
  • Высшая математика

Условие:

Найти общее решение дифференциального уравнения:

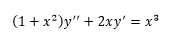
Решение:

Это дифференциальное уравнение второго порядка, допускающее понижение порядка. Так как в уравнение явно не входит функция y, то выполним замену:

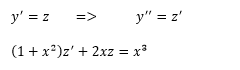
Это линейное неоднородное дифференциальное уравнение.

Найдем общее решение однородного уравнения:

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я