Найти общий интеграл уравнения ydx + x(ln x - y3 )dy = 0 . Условие полного дифференциала не выполняется. Проверим, не допускает ли это уравнение интегрирующего множителя
«Найти общий интеграл уравнения ydx + x(ln x - y3 )dy = 0 . Условие полного дифференциала не выполняется. Проверим, не допускает ли это уравнение интегрирующего множителя»
- Высшая математика
Условие:
Найти общий интеграл уравнения 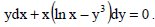
Решение:
Здесь Так как то условие полного дифференциала не выполняется. Проверим, не допускает ли это уравнение интегрирующего множителя. Поскольку приходим к выводу, что данноеуравнение имеет интегрирующий множитель, зависящий только от . Найдем его: Умножая обе части исходного уравнения на найденный интегрирующий множитель получаем уравнение которое, как нетрудно проверить, уже будет уравнением в полных дифференциалах. Решим это уравнение: Взяв в качестве точки (x; y) точку (1;0), имеем следовательно, Это и есть общий интеграл данного уравнения.
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э