Найти стационарные точки функции и исследовать их на экстремум. Абсолютный экстремум функции находится по следующему алгоритму: 1. Найти частные производные 1 – го порядка ;
- Высшая математика
Условие:
Найти стационарные точки функции и исследовать их на экстремум.

Абсолютный экстремум функции находится по следующему алгоритму:
1. Найти частные производные 1 – го порядка 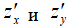 ;
;
2. Приравнять их к нулю и найти все решения этой системы уравнений, полученные точки 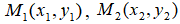 ,… называются критическими точками данной функции;
,… называются критическими точками данной функции;
3. Найти частные производные второго порядка 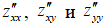 ;
;
рассмотреть первую критическую точку  и вычислить для нее следующие числа:
и вычислить для нее следующие числа:
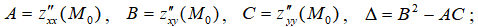
4. Сделать вывод о наличии экстремума в точке 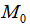 , руководствуясь следующим правилом: если
, руководствуясь следующим правилом: если
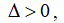
то точка 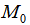 экстремумом не является, если
экстремумом не является, если
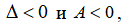
то точка 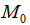 – точка максимума, а если
– точка максимума, а если
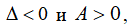
то точка  – точка минимума;
– точка минимума;
5. Аналогично рассмотреть другие критические точки, если они есть.
Решение:
Для заданной функции 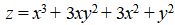
найдем частные производные:
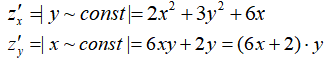
Приравняв частные производные к нулю, получаем систему уравнений:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства