Найти точки разрыва функции. На интервалах (2), (2;0) и (0;) функция непрерывна. Проверке подлежат только точки x 2 и x 0 . Для того чтобы убедиться, что функция непрерывна в точке,
«Найти точки разрыва функции. На интервалах (2), (2;0) и (0;) функция непрерывна. Проверке подлежат только точки x 2 и x 0 . Для того чтобы убедиться, что функция непрерывна в точке,»
- Высшая математика
Условие:
Найти точки разрыва функции.
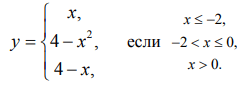
Решение:
На интервалах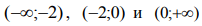 
функция непрерывна.
Проверке подлежат только точки x = - 2и x = 0 .
Для того чтобы убедиться, что функция непрерывна в точке, требуется проверить, равны ли между собой односторонние пределы и равны ли они значению функции в этой точке. Рассмотрим точку
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э