Условие:
Найти три первых отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения y'= f(x,y), удовлетворяющего начальному условию y(0) = y0.
y' = 2ey + xy; y(0) = y.
Решение:
В условиях данной задачи x0 = 0, поэтому общая формула Тейлора
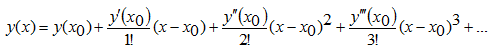
трансформируется в частный случай разложения в ряд Маклорена:
y(0)=0=0. Данное значение равно нулю. По условию требуется найтитри отличных от нуля членов ряда.