1. Главная
  2. Библиотека
  3. Высшая математика
  4. Найти значение биомассы в момент Т=12, если в начальной момент (при t=0) значение биомассы 10. Дифференциальное уравнение....

Найти значение биомассы в момент Т=12, если в начальной момент (при t=0) значение биомассы 10. Дифференциальное уравнение.

«Найти значение биомассы в момент Т=12, если в начальной момент (при t=0) значение биомассы 10. Дифференциальное уравнение.»
  • Высшая математика

Условие:

Требуется составить дифференциальное уравнение динамики развития  некоторого биологического вида и найти решение этого уравнения.

Состояние популяции (в простейшем понимании – стада)  можно охарактеризовать массой m этой популяции (т.е. весом всего стада), причем масса m является функцией времени m = m(t).

Считая, что скорость прироста биомассы пропорциональна биомассе  популяции с коэффициентом k = k(t) и что известна начальная биомасса m0 (при t = 0) найти величину биомассы в момент t = Т.

Найти значение биомассы в момент Т=12, если в начальной момент (при t=0) значение биомассы m0=10  и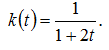

Решение:

Составим дифференциальное уравнение, описывающее динамику развития популяции. Скорость изменения биомассы характеризуется производной m'(t) (при m'0 это скорость развития, при m'0 скорость вымирания). По условию задачи

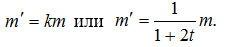
Это уравнение является дифференциальным уравнением с разделяющимися переменными. Разделим переменные m и t:

.

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я