Условие:
Небольшая фирма (игрок А) намерена сбыть партию товара на одном из двух рынков, контролируемых другой, более крупной фирмой (игрок В). Для этого А готова сделать на одном из рынков соответствующие приготовления (например рекламную компанию). Господствующая на рынках фирма (игрок В) может попытаться воспротивиться этому, приняв на одном из рынков предупредительные меры. Не встречая противодействия на рынке, фирма А захватывает его; при наличии препятствий – терпит поражения. Будем считать, для определенности, что проникновение фирмы А на I рынок более важно для нее, нежели на II. Естественно также считать, что и борьба за I рынок потребует вложение больших средств. Например, победа фирмы А на I рынке принесет ей вдвое больше выигрыш, чем победа на втором, но зато и поражение при попытке освоиться на I рынке полностью ее разорит, а фирму В избавит от конкурента. А при поражении фирмы А на II рынке, ее потери будут не столь разорительны, но и победа принесет немного. Пусть матрицы выигрыш для игроков А и В такие:

где А1 – стратегия I игрока освоиться на I рынке, А2 – стратегия I игрока освоиться на II рынке, В1 - стратегия II игрока противостоять на I рынке, В2 – стратегия II игрока противостоять на II рынке.
1) Решить биматричную 2 x 2 задачу со следующими матрицами выигрыши для игроков A и B.
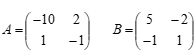
2) Обосновать ответ.
Решение:
Вследствие того, что в биматричных играх интересы игроков не совпадают, необходимо построить такое решение, которое бы в том или ином, но в одинаковом смысле удовлетворяло обоих игроков.
Рассмотрим случай, когда у игроков имеется ровно две стратегии, т.е. m=n=2. В 2x2 биматричной игре платёжные матрицы игроков имеют следующий вид:
A=();B=()
Вероятности р1=р, р2=1-р, q1=q, q2=1-q, а средние выигрыши вычисляются по формулам:
Ha(p,q) = a11p q + a12 p(1-q) + a21(1-p)q + a22(1-p)(1-q),
Hb(p,q) = b11pq + b12 p(1-q) + b21(1-p)q + b22(1-p)(1-q),
где 0 p 1, 0 q 1,
Пара чисел (p*,q*),...
