👋 Решение задач
📚 Высшая математика
решение задачи на тему:
Дата добавления: 10.07.2024
Окружность с центром O вписана в равнобедренную трапецию ABCD с основаниями AD>BC.
а) Докажите, что прямая BO делит площадь трапеции пополам;
б) Пусть M и N – точки касания окружности с боковыми сторонами трапеции. В каком отношении отрезок MN делит площадь трапеции, если AD=3BC?
Ответ
а) Докажите, что прямая BO делит площадь трапеции пополам;
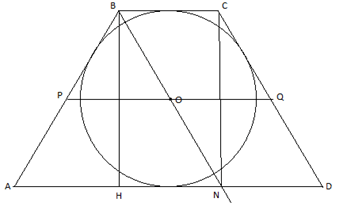
PQ средняя линия; BH=CN высоты
AN=2PO=PQ
SABCD=PQ∙BH
Сводка по ответу
Купи подписку Кампус+ и изучай ответы
Материалы со всех ВУЗов страны
1 000 000+ полезных материалов
Это примеры на которых можно разобраться
Учись на отлично с библиотекой
Набор самых полезных инструментов, работающих на искусственном интеллекте для студентов всего мира.
Экосистема
Кампус
Экосистема сервисов для учебы в удовольствие
Hit
Кампус AI
Твой второй пилот в учебе, быстрые ответы на основе AI
Hit
Кампус Эксперт
ТОП-эксперты помогут решить и объяснят тебе любой вопрос по учебе онлайн
NEW
Кампус Чатс
Сообщество, где ты найдешь знакомства и получишь помощь
Hit
Кампус Хаб
Мультифункциональный умный бот, который всегда под рукой
NEW
Библиотека
База знаний из 1 000 000+ материалов для учебы
