Условие задачи
Определите область (круг) сходимости данного комплексного ряда. Исследуйте его сходимость (сходится абсолютно, сходится условно, расходится) в точках z1, z2, z3.
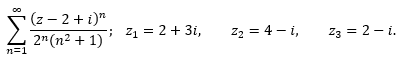
Ответ
Применим признак Даламбера:
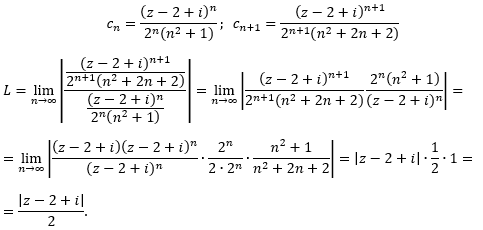
Отсюда заключаем, что ряд сходится абсолютно при условии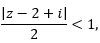 
или внутри круга |z-2+i|2 с радиусом r=2 и с центром в точке z0=2-i.
Исследуем заданные точки.
Потяни
