Условие:
Укажите правильные варианты ответов из предложенных.
1.Определитель 4-го порядка 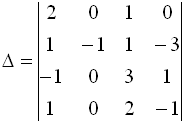 равен
равен
A) 1
B) 0
C) 10
D) 5
2.Определитель 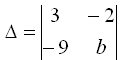 равен нулю при b равном
равен нулю при b равном
A) b=1/6
B) b=6
C) b=-1/6
D) b=-6
3.Определитель матрицы 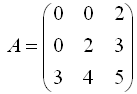 равен
равен
A) -12
B) 12
C) 1
D) 0
4.Для матрицы 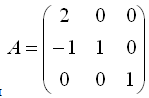 матрица, составленная из алгебраических дополнений, имеет вид
матрица, составленная из алгебраических дополнений, имеет вид
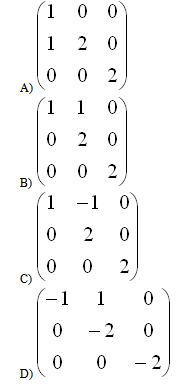
5.Скалярное произведение векторов 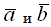 равно -16, угол между ними
равно -16, угол между ними 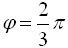 , длина вектора
, длина вектора 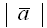 равна 8. Длина вектора
равна 8. Длина вектора 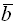 равна
равна
A) 2
B) 6
C) 16
D) 4
6.Проекция вектора 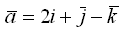 на ось OY равна
на ось OY равна
A) 2
B) 1
C) -1
D) -2
7.Даны векторы 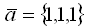 и
и 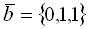 . Скалярное произведение векторов (
. Скалярное произведение векторов ( 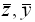 ), где
), где 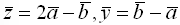 , равно
, равно
A) 2
B) 0
C) -2
D) 1
8.Даны два вектора 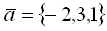 и
и 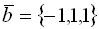 . Векторы
. Векторы 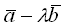 и
и 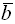 ортогональны, если число
ортогональны, если число 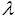 равно
равно
A) -2
B) 1/2
C) 0
D) 2
9.В треугольнике АВС стороны ![]() . Проекция
. Проекция ![]() вектора
вектора ![]() на вектор
на вектор ![]() равна
равна
A) 1
B) 8/3
C) 8
D) 0
10.Даны два вектора ![]() . Скалярный квадрат вектора
. Скалярный квадрат вектора ![]() равен
равен
A) 2
B) 16
C) 26
D) 18
11.Координаты вершин треугольника АВС равны А (1,2,-2), В (2,0,-1), С (2,3,-1). Проекция ![]() стороны
стороны 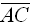 на сторону
на сторону 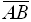 равна
равна
A) 5
B) 0
C) 2
D) 1
12.Даны векторы ![]() . Вектору
. Вектору 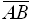 , где точки А (1,1,1) и В (2,-3,2), ортогональны векторы
, где точки А (1,1,1) и В (2,-3,2), ортогональны векторы
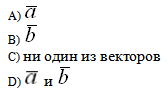
Решение:
1.Определитель 4-го порядка 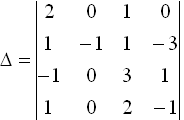 равен
равен
A) 1
B) 0
C) 10
D) 5
2.Определитель 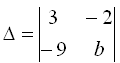 равен нулю при b равном
равен нулю при b равном
A) b=1/6
B) b=6
C) b=-1/6
D) b=-6
3.Определитель матрицы равен
