Условие задачи
По данным выборки, приведенным по вариантам в табл. 4, необходимо:
- определить объем выборки, размах распределения, число интервалов по формуле Стерджеса, шаг ряда и составить вариационный ряд;
- найти средние значения вариантов распределения;
- вычислить относительные частоты; определить моду;
- построить гистограмму вариационного ряда;
- составить эмпирическую функцию распределения;
- построить график эмпирической функции распределения;
- построить кумуляту, определить медиану распределения;
- вычислить несмещенные оценки параметров генеральной совокупности
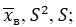 используя средние значения;
используя средние значения; - найти доверительные интервалы для оценки неизвестного математического ожидания α и неизвестного среднего квадратического отклонения σ с заданной надежностью γ = 1-0,01N, где N – номер варианта студента;
- доказать параметрическую гипотезу H0 о равенстве математического ожидания генеральной совокупности значению, выбранному из доверительного интервала для параметра α (задает преподаватель);
- доказать непараметрическую гипотезу о виде закона распределения генеральной совокупности при уровне значимости α = 0.01N .
Выборка:
91, 101, 121, 261, 152, 302, 212, 325, 164, 265, 415, 445, 381, 105, 165, 235, 147, 81, 126, 261, 221, 304, 444, 189, 164, 314, 108, 147, 415, 147, 514, 413, 712, 127, 148, 425, 536, 538, 427, 461, 415, 412, 148, 129, 210, 116, 164, 147, 135, 165, 128, 147, 213, 218, 217, 414, 514, 214, 315, 315, 416, 151, 234, 248, 514, 133, 145, 244, 210, 312, 325, 430, 230, 414
Ответ
1) Упорядочим данные от меньших к большим:
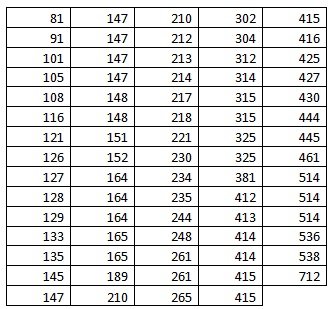
Объем выборки:
n = 74.
Размах распределения:
R = 712 81 = 631.
Число интервалов по формуле Стерджесса:
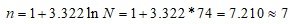
Шаг ряда:









