Условие:
По данным выборки установить теоретический закон распределения случайной величины и проверить согласованность статистического и теоретического распределений по критерию Пирсона при уровне значимости α = 0,05.
Выборка 1
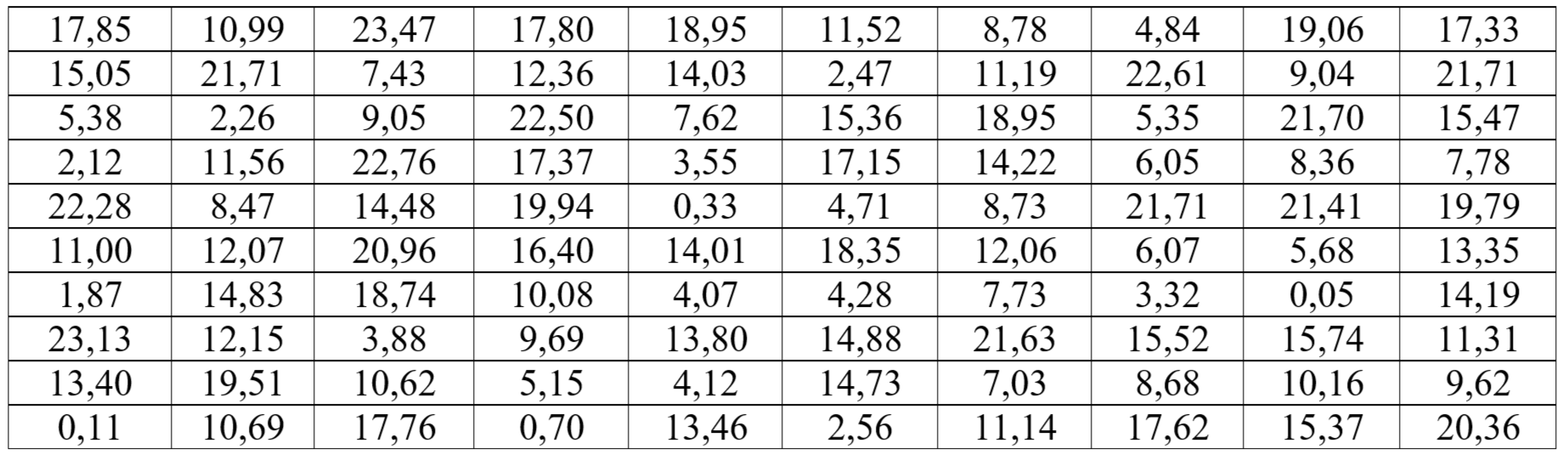
Решение:
1. Найдем наименьшее и наибольшее значения в выборке объема n = 100: хmіn = 0,05 и хmах = 23,47. Округляем эти значения до ближайших целых чисел так, чтобы все статистические значения входили в интервал. Будем исследовать диапазон статистических данных (0; 24) и выберем число частичных интервалов k = 8, а их длина будет h=(24-0)/8=3. Количество интервалов целесообразно брать от 7 до 10 для выборки объема n = 100. Строим интервальный статистический ряд, где Ii разряды, ni частоты каждого интервала, i=ni/n относительные частоты, bi=i/h плотность относительной частоты, а xi* середины частичных ...
