По схеме собственно-случайной бесповторной выборки проведено 10%-ное обследование аптек региона по недельному объему продаж антибиотиков (тыс. руб.). Предполагая, что в регионе функционируют 1000 аптек, получены следующие данные:
- Высшая математика
Условие:
По схеме собственно-случайной бесповторной выборки проведено 10%-ное обследование аптек региона по недельному объему продаж антибиотиков (тыс. руб.). Предполагая, что в регионе функционируют 1000 аптек, получены следующие данные:
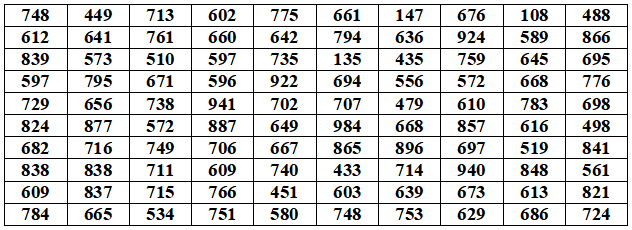
Составить интервальный вариационный ряд. Записать эмпирическую функцию распределения и построить ее график. На одном чертеже изобразить гистограмму и полигон частот.
По сгруппированным данным вычислить выборочные числовые характеристики: среднее арифметическое, исправленную выборочную дисперсию, среднее квадратическое отклонение, коэффициент вариации, асимметрию, эксцесс, моду и медиану.
Заменив параметры генеральной совокупности соответственно их наилучшими выборочными числовыми характеристиками и используя ![]() критерий Пирсона, на уровне значимости
критерий Пирсона, на уровне значимости ![]() проверить две гипотезы о том, что изучаемая случайная величина X – недельный объем продаж антибиотиков – распределена:
проверить две гипотезы о том, что изучаемая случайная величина X – недельный объем продаж антибиотиков – распределена:
а) по нормальному закону распределения;
б) по равномерному закону распределения.
Решение:
Составим интервальное выборочное распределение (интервальный вариационный ряд). Для этого, прежде всего, отметим, что у нас 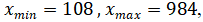 а размах выборочных значений
а размах выборочных значений
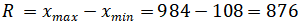
Теперь определим длину каждого частичного интер...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства