Построить корреляционное поле и по визуальной оценке расположенных точек на нем сделать предположение о виде зависимости Y от X. Отдельно рассмотреть резко выделяющиеся наблюдения.
- Высшая математика
Условие:
1. По заданному варианту экспериментальных данных 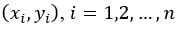 , построить корреляционное поле и по визуальной оценке расположенных точек на нем сделать предположение о виде зависимости от . Отдельно рассмотреть резко выделяющиеся наблюдения.
, построить корреляционное поле и по визуальной оценке расположенных точек на нем сделать предположение о виде зависимости от . Отдельно рассмотреть резко выделяющиеся наблюдения.
2. Вычислить оценки числовых характеристик величин X и Y : эмпирические средние 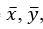 , , эмпирические дисперсии
, , эмпирические дисперсии 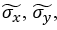 , выборочную ковариацию
, выборочную ковариацию 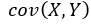 и выборочный коэффициент корреляции
и выборочный коэффициент корреляции 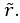 .
.
3. Методом наименьших квадратов найти оценки коэффициентов a и b уравнения эмпирической регрессии. Записать уравнение эмпирической регрессии y = a=bx .
4. Предсказать значение y* для заданного 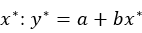 . Вычислить
. Вычислить 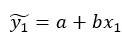 , погрешность
, погрешность 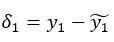 и относительную погрешность
и относительную погрешность 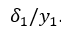
5. Построить прямую эмпирической регрессии y = a=bx по точкам (x1,y1 ) и (x*,y*) на корреляционном поле.
6. Оценить качество модели: вычислить коэффициент детерминации R2 ; определить значимость уравнения регрессии по критерию Фишера на уровне значимости a =0.05.
7. а) вычислить среднеквадратические ошибки определения коэффициентов a и b , определить значимость коэффициентов по критерию Стьюдента на уровне значимости a = 0.05 . б) построить доверительный интервал для прогноза y* и доверительную полосу для среднего значения СВ Y , соответствующие доверительной вероятности 0,95.
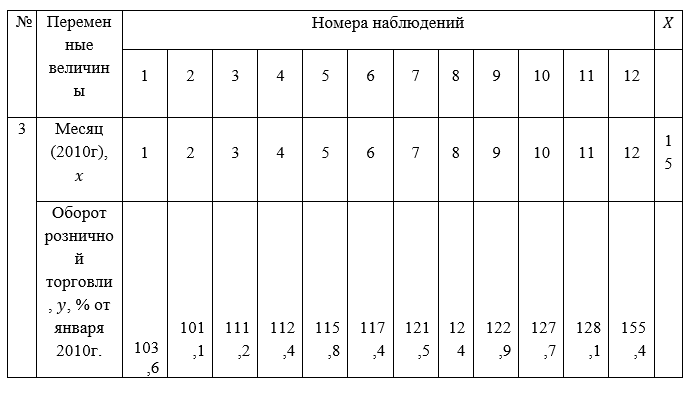
Решение:
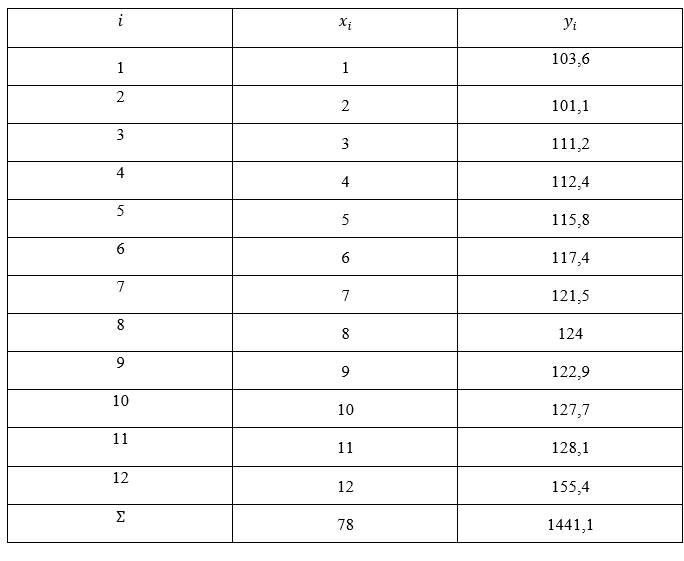
Построим диаграмму рассеяния в excel (поле корреляции):
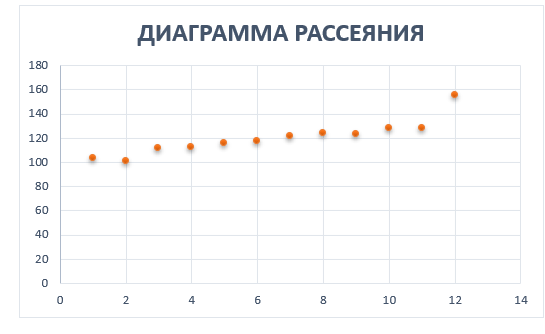
На основании визуального исследования выдвинем гипотезу о линейной зависимости Y от X :
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства