Построить на плоскости область допустимых решений системы линейных неравенств, найти наибольшее и наименьшее значения линейной функции Z(X). Z = -x_1 – x_2 .
«Построить на плоскости область допустимых решений системы линейных неравенств, найти наибольшее и наименьшее значения линейной функции Z(X). Z = -x_1 – x_2 .»
- Высшая математика
Условие:
Построить на плоскости область допустимых решений системы линейных неравенств, найти наибольшее и наименьшее значения линейной функции Z(X).
Z = -x1 – x2 .
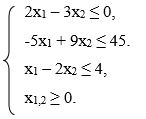
Решение:
Количество переменных равно двум, поэтому задачу линейного программирования можно решить графическим методом, т.к. область решения можно изобразить на плоскости.
Каждое неравенство ограничений представляет собой полуплоскость, граница которого выражается строгим равенством:
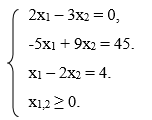
Построим границы, которые представляют собой прямые, заданные этим уравнениями. Для построения прямой линии необходимо найти ко...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э