Решение задачи
Постройте фактор-группу аддитивной группы целых чисел по ее нормальной подгруппе М и найдите элементы, противоположные 3 ̅,4 ̅, в каждом случае: 1) M=〈5〉; 2) M=〈7〉.
- Высшая математика
Условие:
Постройте фактор-группу аддитивной группы целых чисел по ее нормальной подгруппе М и найдите элементы, противоположные 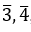 в каждом случае:
в каждом случае:
1) M=⟨5⟩; 2) M=⟨7⟩.
Решение:
Поскольку 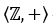 абелева группа, то любая её подгруппа нормальна. Если , то множество кратных . В смежный класс по подгруппе попадают те элементы, разность которых кратна , т.е. которые при делении с остатком на дают одинаковый остаток. Таким образом, смежные классы по подгруппе n это классы вычетов по модулю.
абелева группа, то любая её подгруппа нормальна. Если , то множество кратных . В смежный класс по подгруппе попадают те элементы, разность которых кратна , т.е. которые при делении с остатком на дают одинаковый остаток. Таким образом, смежные классы по подгруппе n это классы вычетов по модулю.
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
Р
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э