Условие:
Предприятию нужно перевести со склада по железной дороге изделия трех различных видов: Изделий I –го вида не более 640, изделий II-го вида не более 800, изделий III-го вида не более 860.
Подразделение железной дороги может для этой перевозки выделить специально оборудованные вагоны двух типов А и В. Для полной загрузки вагона следует помещать в него изделия всех трех видов. При этом в вагон типа А входят 1 изделий I-го вида, 5 изделий II-го вида, 3 изделий III-го вида; в вагон типа B входят 4 изделий I-го вида, 2 изделий II-го вида, 5 изделий III-го вида.
Экономия от перевозки груза в вагоне типа А составляет 20 руб., в вагоне типа В – 13 руб.
Сколько вагонов каждого типа следует выделить для перевозки, чтобы суммарная экономия от перевозки груза была наибольшей?
Задачу решить симплекс методом путем преобразования симплекс- таблиц и геометрическим методом.
Решение:
Оформим данные задачи в виде таблицы.
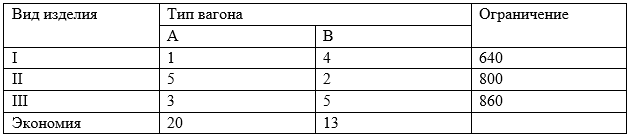
Обозначим: x1 (ед) количество вагонов типа А; x2 (ед) количество вагонов типа В; F (руб) суммарная экономия от перевозки груза.
Совокупность неизвестных (х1, х2) называется планом производства.
Очевидно, должны соблюдаться условия неотрицательности: