Представьте в тригонометрической форме следующие числа: n; -m; ik; -in; 1+i; 1-i; 1+√3 i; √3-i; m+ki. а) z = 4 б) z = -2 в) z = 5i

а) z = 4

Находим тригонометрическую форму комплексного числа z = 4

Действительная часть числа x.

x = Re(z) = 4

Мнимая часть числа y.

y = Im(z) = 0

Модуль комплексного числа |z|.

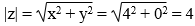
Поскольку x 0, y 0, то arg(z) находим как: