Применяя равносильные преобразования, доказать тождественную истинность формул:а) (x→y)∨(y→x); б) x ̄yz ̄∨x ̄yz∨x∨y ̄; в) x ̄y ̄z ̄∨x ̄y ̄z∨x ̄yz ̄∨x ̄yz∨x; г) (x↔y)y ̄→x ̄.

Условие:

Применяя равносильные преобразования, доказать тождественную истинность формул:

а) (x→y)∨(y→x); б) x ̄yz ̄∨x ̄yz∨x∨y ̄;

в) x ̄y ̄z ̄∨x ̄y ̄z∨x ̄yz ̄∨x ̄yz∨x; г) (x↔y)y ̄→x ̄.

а) (xy)(yx)

Выпишем основные логические равносильности:

Закон двойного отрицания:

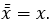
Идемпотентность:

xxx=x, xx...x=x.

Коммутативность:

xy=yx, xy=yx.

Ассоциативность:

x(yz)=(xy)z, x(yz)=(xy)z.

Дистрибутивность:

x(yz)=(xy)(xz), x(yz)=(xy)(xz).

Законы де Моргана: