Решение задачи
Применив процесс ортогонализации, построить ортонормированный базис n-мерного пространства, натянутого на заданную систему векторов (скалярное произведение стандартное).
- Высшая математика
Условие:
Применив процесс ортогонализации, построить ортонормированный базис n-мерного пространства, натянутого на заданную систему векторов (скалярное произведение стандартное).
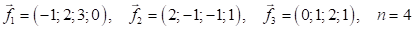
Решение:
Найдем базис заданной линейной оболочки, для чего приведем матрицу к ступенчатому виду:
Получили ступенчатый вид, состоящий из трех строк, значит, ранг матрицы равен трем и все три вектора линейно независимы и входят в базис линейной оболочки.
Построим для начала ортогональный базис
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
Р
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э