Условие задачи
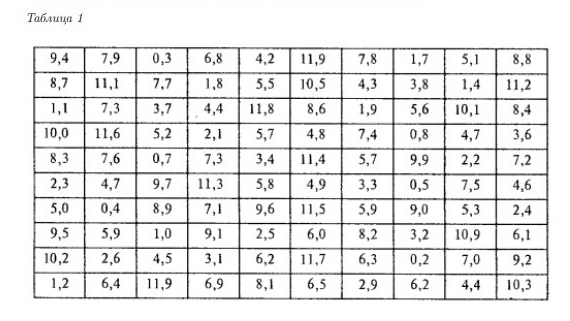
В результате эксперимента получены статистические данные (таблица 1).
Требуется:
1) записать значения результатов эксперимента в виде вариационного ряда;
2) найти размах варьирования и разбить его на интервалы, используя
- формулу Стёрджеса;
- либо любую другую формулу, либо подобрать нужное число вручную;
3) построить интервальный статистический ряд, полигон частот, гистограмму относительных частот;
4) найти эмпирическую функцию распределения и построить её график;
5) найти числовые характеристики выборки: выборочное среднее, выборочную дисперсию, выборочную исправленную дисперсию;
a) найти доверительный интервал при надежности p=0,9 для математического ожидания;
6) приняв в качестве нулевой гипотезы H0: {генеральная совокупность, из которой извлечена выборка, имеет равномерное распределение}, проверить её, пользуясь критерием Пирсона при уровне значимости A=0,01.
Ответ
1) запишем значения результатов эксперимента в виде вариационного ряда (упорядочим по возрастанию):
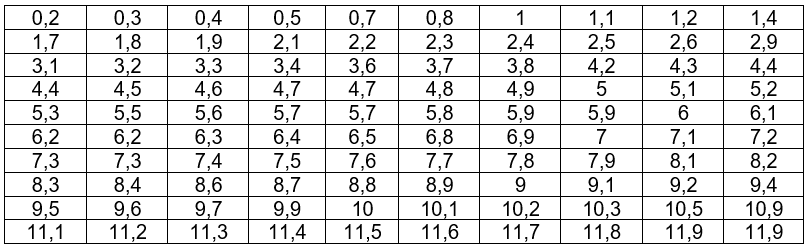
n=100
2) найдем размах варьирования и разобьем ряд на интервалы, используя формулу Стёрджеса:
xmin, xmax, l=11,9-0,2=11,7
k=1+log2n8
