Проанализируйте и определите тип дифференциального уравнения первого порядка и найдите его общее решение. Данные указаны ниже.

Делим обе части уравнения на х:

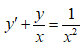(1)

Это линейное дифференциальное уравнение 1-го порядка вида

y'+ P(x)y = Q(x), гдe P(x)=1/х; Q(x)= 1/х²

Общее решение находим с помощью подстановки :

y = u(x)v(x) (2)

тогда y' =u'v+uv' (3)

Подставляя выражения (2) и (3) в уравнение (1), получим: