Проинтегрировать уравнение. Непосредственной проверкой легко убедиться, что x = 0 и u = 1 т. е. y = x , являются также решениями данного уравнения, но они не входят в общий интеграл. Такие решения называются особыми.
«Проинтегрировать уравнение. Непосредственной проверкой легко убедиться, что x = 0 и u = 1 т. е. y = x , являются также решениями данного уравнения, но они не входят в общий интеграл. Такие решения называются особыми.»
- Высшая математика
Условие:
Проинтегрировать уравнение: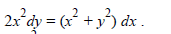 
Решение:
Разделив обе части уравнения на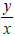 
dx, получим уравнение, правая часть которого есть функция отношения
или Положим в немтогда y = ux, дифференцируем , получим уравнение с разделяющимися переменными:После разделения переменных получим уравнение с разделенными переменными:Интегрируем , подставим , получим:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э