Условие задачи
Пусть S - канторова лестница.
(a) S является графиком некоторой функции у = s(x) (то есть прямая х = k при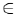 
[0, 1] пересекает S ровно в одной точке).
(b) Покажите, что функция s(x) неубывающая.
(с) Докажите, что у = s(x)- непрерывная функция.
(d) Объясните, как по троичной записи х построить у = s(x).
(e) Посчитайте длину ломаной с вершинами в точках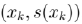 
, где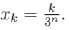 
(f) Длина кривой S не больше 2. (Подсказка: пусть есть какая-то ломаная, впи- саная в S, рассмотрите проекции ее звена на оси координат, вспомните теорему Пифагора и воспользуйтесь монотонностью.)
(g) Длина кривой S равна 2.
Ответ
(a) Рассмотрим пару последовательностей функций
𝑓𝑛(𝑥) = inf{𝑦 : (𝑥, 𝑦) 𝑆𝑛}, 𝐹𝑛(𝑥) = sup{𝑦 : (𝑥, 𝑦) 𝑆𝑛}, 𝑛 0.
Согласно построению, функции {𝑓𝑛(𝑥)} непрерывны слева, а функции {𝐹𝑛(𝑥)} справа, и те и другие являются неубывающими и
𝑆𝑛 = {(𝑥, 𝑦) : 𝑥 [0; 1], 𝑓𝑛(𝑥) 𝑦 𝐹𝑛(𝑥)}.
Далее отметим, что 𝑓𝑛(𝑥) = 𝐹𝑛(𝑥) при 𝑥 𝐺𝑛 и
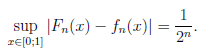
Таким образом, последовательности функций {𝑓𝑛(𝑥)} и {𝐹𝑛(𝑥)} сходятся пот...
