Условие задачи
Распределение 50 городов по численности населения ξ (тыс. чел.) и среднемесячному доходу на одного человека η (тыс. руб.) представлено в таблице:
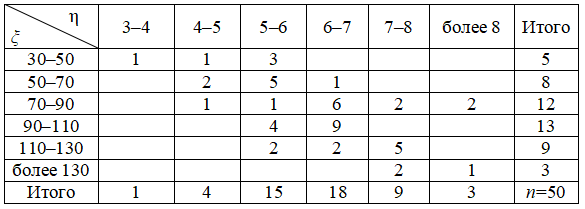
Необходимо:
1) вычислить групповые средние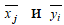 
, построить эмпирические линии регрессии;
2) предполагая, что между переменными ξ и η существует линейная корреляционная зависимость:
а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать содержательную интерпретацию полученных уравнений;
б) вычислить коэффициент корреляции, на уровне значимости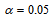 
оценить его значимость и сделать вывод о тесноте и направлении связи между переменными ξ и η;
в) используя соответствующее уравнение регрессии, оценить средний доход на одного человека в городе с населением 100 тыс. человек.
Ответ
1) Полученные в ходе обследования эмпирические
данные представляют собой двумерную выборку, объем которой равен 50. По каждой переменной они представляют собой интервальный вариационный ряд. Для упрощения дальнейшей обработки заменим интервальные вариационные ряды их дискретными аналогами. Для этого каждый интервал разбиения, как по переменной x, так и по переменной h , будем характеризовать их срединным значением, для этого вычислим середины каждого интервала. Обозначим варианты переменной через , а варианты переменной через . Получим:
