Условие задачи
Выполнить разложение функции в ряд Фурье
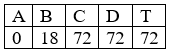
Задана непрерывная слева, кусочно-линейная на отрезке [0,T] функция f(x).
Эта функция равна нулю на интервалах (0,A) и (D,T) и равна единице на интервале (B,C).
Если A = 0 или D = T, то f(x) = 0 при x = 0 или x = T соответственно.
Если B = C, то f(x) = 1 при x = B.
На отрезке [A,B] f(x) изменяется линейно от 0 до 1,
если A = B, то f(x) имеет в точке x = A разрыв.
На отрезке [C,D] f(x) изменяется линейно от 1 до 0.
Если С = D, то f(x) имеет в точке С разрыв.
Построить график функции f(x).
Разложить функцию f(x) в неполные ряды Фурье двумя способами:
1) по косинусам, т.е. в системе
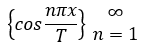
2) по синусам, т.е. в системе
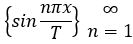
Для каждого разложения построить на одном чертеже на отрезке [-3 T; 3 T] графики первых трех частичных сумм и график суммы ряда Фурье.
Введите результаты расчета с точностью ε = 10-3 (3 десятичных знака после запятой).
Ответ
Выражение для f(x) имеет вид
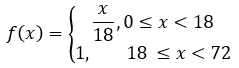
График функции f(x) построен на рис. 1.
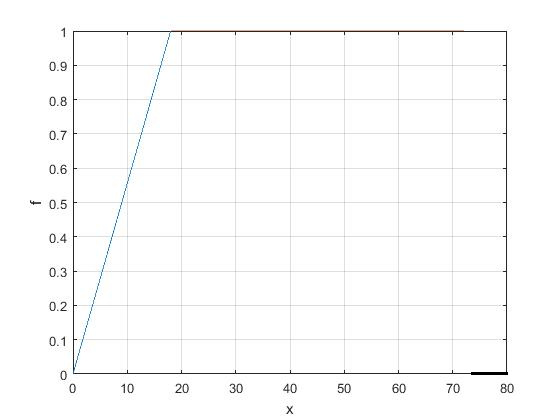
Рис. 1
Найдем коэффициенты разложения в ряд Фурье по косинусам.
