Условие:
Решить дифференциальные уравнения:
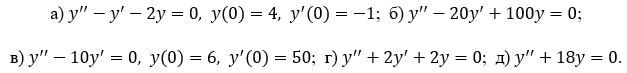
Решение:
Все пять уравнений являются линейными однородными дифференциальными уравнениями второго порядка с постоянными коэффициентами. Решения будем получать, путем отыскания корней соответствующего характеристического уравнения, для которых будем записывать фундаментальную систему частных решений и соответствующее общее решение. При необходимости найдем произвольные постоянные из начальных условий.
Характеристическое уравнение имеет вид Так как корни действительные и различные, то фундаментальная система частных решений состоит из двух линейно независимых частных решений данного ДУ:а общее решение явля...
