Условие:
Решить элементарную экономико-математическую задачу графическим методом.
При помощи графических построений на плоскости найти неотрицательные значения переменных, при которых целевая функция приобретает экстремальное значение (достигает MAX или MIN).
| ОГРАНИЧЕНИЕ | ПЕРЕМЕННАЯ 1 | ПЕРЕМЕННАЯ 2 | Тип ограничения | Объем ограничения |
| A | 4 | 5 | Не более | 85 |
| B | -8 | 12 | Не более | 75 |
| C | 3 | 5 | Не менее | 20 |
| D | 6 | -8 | Не более | 24 |
| E | -2 | 10 | Не менее | 18 |
|
Целевая функция |
12 | -8 | MAX, MIN | MAX, MIN |
Решение:
Найдем экстремальное решение задачи, математическая модель которой имеет вид
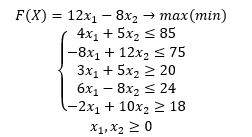
Введем систему декартовых координат на плоскости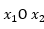 
, и построим области, описываемые системой ограничений.
Каждое неравенство ...