1. Главная
  2. Библиотека
  3. Высшая математика
  4. Решить систему уравнений: {(x^'=4x-y, @y^'=-x+4y.)┤Дифференцируя первое уравнение системы, получим x^''=4x^'-y^'. В это...

Решить систему уравнений: {(x^'=4x-y, @y^'=-x+4y.)┤Дифференцируя первое уравнение системы, получим x^''=4x^'-y^'. В это уравнение подставим y^' из второго

«Решить систему уравнений: {(x^'=4x-y, @y^'=-x+4y.)┤Дифференцируя первое уравнение системы, получим x^''=4x^'-y^'. В это уравнение подставим y^' из второго»
  • Высшая математика

Условие:

1. Решить систему уравнений:  

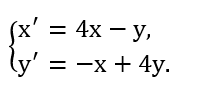
Решение:

Дифференцируя первое уравнение системы, получим:

x'' = 4x' - y'.

В это уравнение подставим y' из второго уравнения, тогда:

x'' = 4x'-(-x+4y) = 4x'+x-4y.

В это уравнение подставим y, найденное из первого уравнения системы, то есть

x'' = 4x'- 4(4x-x' );x''- 8x'...

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я