Условие:
Решить уравнение: 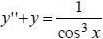 .
.
Решение:
Данное уравнение является линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Его общее решение будем искать в виде: . Составим однородное уравнение, соответствующее исходному: . Его характеристическое уравнение имеет комплексно-сопряженные корни , которым соответствует фундаментальная система решений: = cosx, = sinx. Следовательно, общее решение однородного уравнения имеет вид:
