Решить задачу линейного программирования графическим методом с использованием вектора нормали (градиента) и линии уровня целевой функции. Построить и четко обозначить
- Высшая математика
Условие:
Решить задачу линейного программирования графическим методом с использованием вектора нормали (градиента) и линии уровня целевой функции. Построить и четко обозначить полуплоскости, область допустимых решений, линии уровня и вектор градиент целевой функции. Обосновать полученное решение.
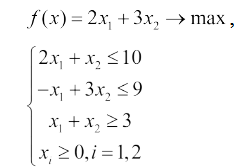
Решение:
Необходимо найти максимальное значение целевой функции F = 2x1+3x2 max, при системе ограничений:
2x1+x210, (1)
-x1+3x29, (2)
x1+x23, (3)
x1 0, (4)
x2 0, (5)
Запишем уравнения граничных прямых и построим их на плоскости x10x2.
2x1+x2=10, (1)
-x1+3x2=9, (2)
x1+x2=3, (3)
x1 0, (4)
x2 0, (5)
Построим уравнение 2x1+x2 = 10 по двум точкам. Для нахождения первой точки приравниваем x1 = 0. Находим x2 = 10. Для нахождения второй точки приравниваем x2 = 0. Находим x1 = 5. Соединяем точку (0;10) с (5;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), опр...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства