Главная
Библиотека
Высшая математика
С целью определения средней величины месячной заработанной платы работников торговой сферы в некотором крупном районе горо...

С целью определения средней величины месячной заработанной платы работников торговой сферы в некотором крупном районе города, по схеме собственно-случайной бесповторной выборки было отобрано 150 работников из 1300.

«С целью определения средней величины месячной заработанной платы работников торговой сферы в некотором крупном районе города, по схеме собственно-случайной бесповторной выборки было отобрано 150 работников из 1300.»

30 апреля 2024
Высшая математика

Условие:

С целью определения средней величины месячной заработанной платы работников торговой сферы в некотором крупном районе города, по схеме собственно-случайной бесповторной выборки было отобрано 150 работников из 1300. Распределение месячной заработной платы (тыс. руб.) представлено в таблице:

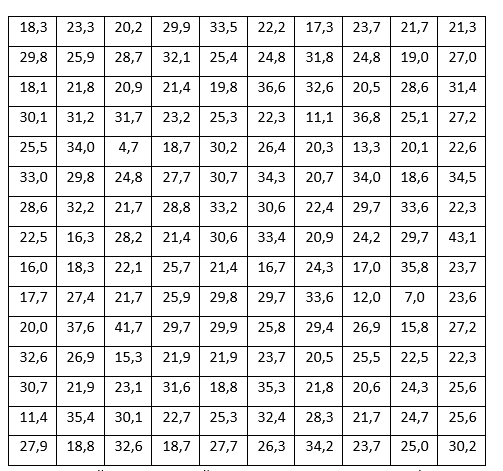
Составить интервальный вариационный ряд. Записать эмпирическую функцию распределения и построить ее график. На одном чертеже изобразить гистограмму и полигон частот.

По сгруппированным данным вычислить выборочные числовые характеристики: среднее арифметическое, исправленную выборочную дисперсию, среднее квадратичное отклонение, коэффициент вариации, асимметрию, эксцесс, моду и медиану.

Решение:

Объем выборки n = 150, x_min = 4,7, x_maх = 43,1 . Определим оптимальное число интервалов по формуле Стерджесса:

1 + log₂n = 1 + log₂150 8,22

Округляя до ближайшего целого, получим k = 8 интервалов. Длина интервала:

l = (x_max - x_min) / k = (43,1 - 4,7) / 8 = 4,8

Разобьем отрезок [4,7; 43,1] на интервалы длины l = 4,8 м . Подсчитаем частоты попадания значений выборки в интервалы. Построим интервальный вариационный ряд. Найдем относительные частоты wi = ni / n , накопленные от...