Условие:
С помощью критерия устойчивости Гурвица исследовать устойчивость системы, дифференциальное уравнение которой:
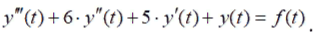
Решение:
В соответствии с критерием Гурвица, САУ будет устойчивой, т.е. корни характеристического уравнения
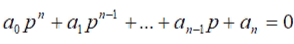
будет иметь отрицательные действительные части, если определитель Гурвица и все диагональные миноры положительны.
Порядок составления определителя Гурвица: Все коэффициенты от а1 до аn располагаются в порядке возрастания по главной диагонали. Вверх от главной диагонали в столбцах записываются коэффицие...