1. Главная
  2. Библиотека
  3. Высшая математика
  4. Сгруппировать эти данные в интервальную таблицу, подобрав длину интервала, построить гистограмму, полигон частот и эмпирич...

Сгруппировать эти данные в интервальную таблицу, подобрав длину интервала, построить гистограмму, полигон частот и эмпирическую функцию распределения.

«Сгруппировать эти данные в интервальную таблицу, подобрав длину интервала, построить гистограмму, полигон частот и эмпирическую функцию распределения.»
  • Высшая математика

Условие:

Известны  x1,x2,…,xn- результаты независимых наблюдений над случайной величиной X.

Сгруппировать эти данные в интервальную таблицу, подобрав длину интервала.
Построить гистограмму, полигон частот и эмпирическую функцию распределения.
Найти несмещённые оценки для математического ожидания и дисперсии случайной величины X. Указать моду M0.
По критерию х2 (Пирсона) проверить гипотезу о том, что случайная величина X имеет нормальный закон распределения.
Найти интервальные оценки математического ожидания и дисперсии случайной величины X с уровнем доверия γ=0,9.

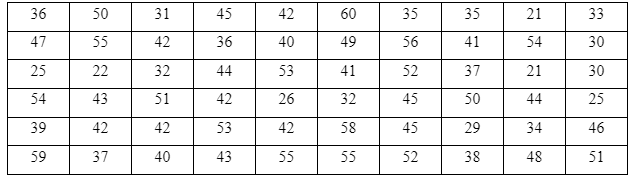
Решение:

Объем выборки равен n=60

Сгруппируем данные в интервальную таблицу:

Определим число интервалов по формуле Стерджеса:

N=1+3,322lg n =1+3,322lg 60 =1+3,322∙1,7786,97

Выделим 7 интервалов.

Рассчитаем величину каждого интервала, для этого найдем размах выборки:

xmax=60 xmin=21

Размах выборки:

R=xmax-xmin=60-21=39

Величина интервала:

l=R/N=39/7=5,6

Примем x0=xmin', x1=x0+l,

Посчитаем количество вхождений вариант в каждый из интервалов.

Интервальный ряд распределения:

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я