Условие задачи
Случайная величина ξ имеет нормальный закон распределения с параметрами а и σ2. Найти параметр σ, если известно, что М(ξ)=5 и P( 2 < ξ < 8 ) = 0, 9973.
Вычислить вероятность того, что значение случайной величины ξ окажется меньше 0.
Построить графики функции распределения и функции плотности распределения этой случайной величины.
Ответ
Для нормально распределенной случайной величины вероятность ее попадания на интервал находится с помощью функции Лапласа Ф(х) по формуле:
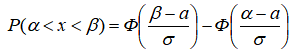
Если P( 2 8 ) = 0,9973, то для заданного параметра а =М()=5 (математическое ожидание известно), можно записать уравнение, из которого найдем неизвестное среднее квадратическое ожидание :
Потяни
