Условие:
Случайная величина X задана интегральной функцией распределение F(x).
Найти: а) дифференциальную функцию f(x); б) математическое ожидание M(X) и дисперсию D(X); в) построить графики f(x) и F(x).
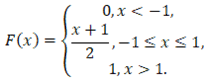
Решение:
а) дифференциальную функцию f(x)
Дифференциальная функция распределения равна первой производной от интегральной функции распределения
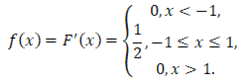
По виду дифференциальной функции распределения можно сделать вывод, что случайная величина распределена равномерно в интервале [-1;1].
б) математическое ожидание M(X) и дисперсию D(X)
Математическое ожидание
