1. Главная
  2. Библиотека
  3. Высшая математика
  4. Составить интервальный вариационный ряд для фактора X, найти его основные числовые характеристики (мода, медианна, выбороч...

Составить интервальный вариационный ряд для фактора X, найти его основные числовые характеристики (мода, медианна, выборочное среднее, эмпирическую дисперсию, коэффициенты асимметрии и эксцесса), построить графики гистограммы, полигона частот и кумуляты.

«Составить интервальный вариационный ряд для фактора X, найти его основные числовые характеристики (мода, медианна, выборочное среднее, эмпирическую дисперсию, коэффициенты асимметрии и эксцесса), построить графики гистограммы, полигона частот и кумуляты.»
  • Высшая математика

Условие:

Составить интервальный вариационный ряд для фактора X, найти его основные числовые характеристики (мода, медианна, выборочное среднее, эмпирическую дисперсию, коэффициенты асимметрии и эксцесса), построить графики гистограммы, полигона частот и кумуляты.

2) Проверить гипотезу о нормальном распределении фактора X по критерию Пирсона при уровне значимости   

3) Построить доверительные интервалы для математического ожидания и дисперсии.

4) Найти выборочный коэффициент корреляции и построить доверительный интервал для него.

5) Составить уравнение линейной регрессии и построить поле регрессии и линию регрессии на одном графике.

Решение:

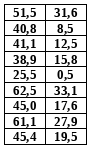
1) Составим интервальный ряд для величины X. Для этого определим наибольшее и наименьшее значения величины X, встречающееся в выборке.

xmax =70.2; xmin =25.5

Вычислим размах:

R= xmax - xmin =70.2-25.5=44.7

Теперь определим длину каждого частичного интервала (иногда их называют классовыми интервалами), воспользовавшись формулой Стерджеса:

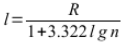
где n объем выборки. В нашем случае

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я