Составить план перевозки продукции, при котором минимизируются суммарные затраты по ее изготовлению и доставке потребителям для условия что продукция.
- Высшая математика
Условие:
В пунктах Аi (i=1, 2, 3) производится однородная продукция в количестве аi единиц. Себестоимость единицы продукции в i-м пункте равна Ci. Готовая продукция поставляется в пункты Вj (j=1, 2, 3, 4), потребности которых составляют bj ед. Cтоимость перевозки единицы продукции из пункта Ai в пункт Bj задана матрицей Cij.
Требуется:
1) Написать математическую модель прямой и двойственной задач с указанием экономического смысла всех переменных;
2) Составить план перевозки продукции, при котором минимизируются суммарные затраты по ее изготовлению и доставке потребителям для условия что продукция, произведенная в пункте Ai, где себестоимость её производства наименьшая, распределяется полностью;
3) Вычислить суммарные минимальные затраты Zmin;
4) Узнать в какие пункты развозится продукция от поставщиков;
5) Установить пункты, в которых останется нераспределенная продукция, и указать её объем.
Необходимые исходные числовые данные приведены в таблице.
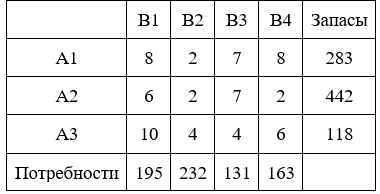
Решение:
Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов
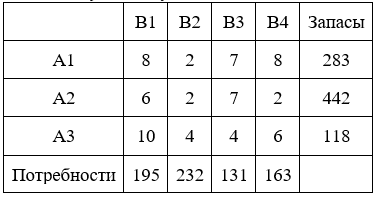
Себестоимости единицы продукции в i-м пункте равны Ci: 2, 5, 1.
Математическая модель транспортной задачи:
F = cijxij, (1)
при условиях:
xij = ai, i = 1,2,, m, (2)
xij = bj, j = 1,2,, n, (3)
xij 0
Запишем экономико-математическую модель для нашей з...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства