Составьте вариационный ряд, постройте полигон и гистограмму, полагая начало первого интервала: 0, длина интервала: 1. Найдите эмпирическую функцию распределения и постройте ее график.
- Высшая математика
Условие:
Дана выборка значений случайной величины:
0, 4, 2, 0, 5, 1, 1, 3, 0, 2, 2, 4, 3, 2, 3, 3, 0, 4, 5, 1, 3, 1, 5, 2, 0, 2, 2, 3, 2, 2, 2, 6, 2, 1, 3, 1, 3, 1, 5, 1, 5, 5, 3, 2, 2, 0, 2, 1, 1, 3, 2, 3, 5, 3, 5, 2, 5, 2, 1, 1, 2, 3, 4, 3, 2, 3, 2, 4, 2.
Для данной выборки.
Составьте вариационный ряд, постройте полигон и гистограмму, полагая начало первого интервала: 0, длина интервала: 1.
Найдите эмпирическую функцию распределения и постройте ее график.
Вычислите: 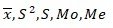
Проверьте гипотезу о распределении Пуассона соответствующей генеральной совокупности при уровне значимости α=0,01
Решение:
Объем выборки: n=69
1) Так как случайная величина принимает ограниченное количество значений, то составим дискретный вариационный ряд. Подсчитаем количество вхождений каждого значения случайной величины:

Построим полигон частот ломанную с координатами вершин (xi;ni )
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства