Условие задачи
Установить, какую кривую определяет данное уравнение: 9x2-36y2+72x+72y+432=0
Найти:
1) координаты её центра C;
2) полуоси кривой;
3) координаты фокусов;
4) эксцентриситет;
5) уравнение директрисы;
6) уравнение асимптот (для гиперболы);
7) сделать чертёж.
Ответ
1) Линия определяет кривую гиперболического типа, если A и C имеют разные знаки, поэтому в данном случае у нас кривая гиперболического типа.
Приведём уравнение к каноническому виду:
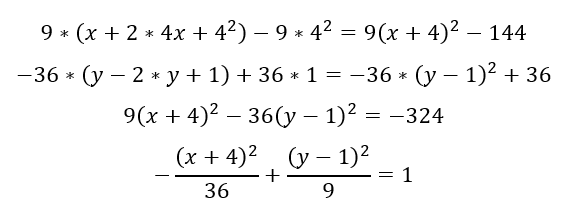
Получили каноническое уравнение гиперболы с центром в точке C (-4; 1).
2) Полуоси кривой выглядят так:
a = 6 (мнимая полуось)
b = 3 (действительная полуось)
Потяни
