Условие задачи
В декартовой прямоугольной системе координат даны вершины пирамиды:
A(-3;1;1),B(0;-4;-1),C(5;1;3), D(4;6;-2). Найдите:
а) длину ребра AB;
б) косинус угла между векторами AB и AC;
в) уравнение ребра AB;
г) уравнение грани ABC;
д) уравнение высоты, опущенной из вершины D на грань ABC;
е) координаты векторов e1=AB, e2=AC, e3=AD и докажите, что они образуют линейно независимую систему;
ж) координаты вектора MN, где M и N – середины рёбер AD и BC соответственно;
з) разложите вектор MN по базису
Ответ
Запишем координаты векторов:
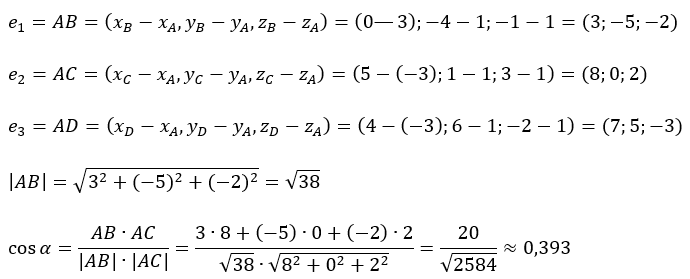
уравнение ребра AB запишем по направляющему вектору и точке A:
Уравнение грани, проходящей через три точки, найдем по формуле:
Потяни
