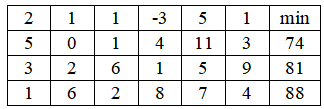
В каждом варианте приведены таблицы, в которых записаны условия канонической задачи линейного программирования на минимум, т. е. В первой строке помещены коэффициенты целевой функции.
- Высшая математика
Условие:
В каждом варианте приведены таблицы, в которых записаны условия канонической задачи линейного программирования на минимум, т. е. ![]() В первой строке помещены коэффициенты целевой функции. В остальных строках, в первых пяти столбцах, находятся векторы условий, а в последнем столбце записан вектор ограничений. В правом верхнем углу таблицы указана цель задачи.
В первой строке помещены коэффициенты целевой функции. В остальных строках, в первых пяти столбцах, находятся векторы условий, а в последнем столбце записан вектор ограничений. В правом верхнем углу таблицы указана цель задачи.
Необходимо последовательно выполнить следующие задания.
1. Задачу решить графическим методом.
2. Применяя симплекс-метод, решить задачу или установить, что задача не имеет решения. Начальный план рекомендуется искать методом искусственного базиса.
3. Построить двойственную задачу. Если вектор 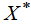 найден, вычислить оптимальный план
найден, вычислить оптимальный план 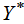 двойственной задачи, используя первую теорему двойственности
двойственной задачи, используя первую теорему двойственности 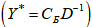 . Вычислить значение функции
. Вычислить значение функции 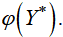
4. Провести анализ полученного решения, применяя условия дополняющей нежесткости.
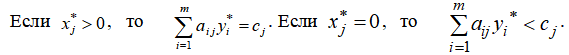
Решение:
Требуется определить минимальное значение целевой функции F(X) = 2x1 + x2 + x3 - 3x4 + 5x5 + x6 при следующих условиях-ограничений.
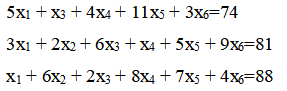
Решить данную задачу графически нельзя, так как мы имеем 6 переменных и только 3 условия. Поэтому решаем задачу симплекс-методом.
Введем искусственные переменные x: в 1-м равенстве вводим переменную x7; в 2-м равенстве вводим переменную x8; в 3-м равенстве вводим ...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства