В некоторой декартовой системе координат известно соотношение. Известно, что Ai и Bik составляют компоненты тензоров I-го и II-го рангов соответственно. Доказать, что Mijk − тензор III-го ранга.
«В некоторой декартовой системе координат известно соотношение. Известно, что Ai и Bik составляют компоненты тензоров I-го и II-го рангов соответственно. Доказать, что Mijk − тензор III-го ранга.»
- Высшая математика
Условие:
В некоторой декартовой системе координат известно соотношение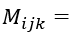 
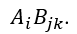. Известно, что Ai и Bik составляют компоненты тензоров I-го и II-го рангов соответственно. Доказать, что Mijk − тензор III-го ранга.
Решение:
Далее везде в индексных формулах используем правило Эйнштейна, по дважды повторяющемуся индексу предполагается суммирование.
Поскольку Ai тензоров I-го ранга, то его компоненты в двух базисах связаны соотношениями:
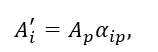
где компоненты матрицы преобразования от одного базиса к другому.
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э