Условие задачи
В первой урне 12 белых и 4 чёрных шара. Во второй 4 белых и 5 чёрных шара. Из первой урны вынимают случайным образом 3 шара, из второй 3. Найти вероятность того, среди вынутых шаров:
a) все шары одного цвета;
б) только три белых шара;
в) хотя бы один белый шар.
Ответ
a) Обозначим событие А: среди вынутых шаров все шары одного цвета. Тогда события:
А1 из первой урны вынули 3 белых шара, А2 из второй - 3 белых шара, А3 из первой урны вынули 3 чёрных шара, А4 из второй 3 чёрных шара. Так как события А1 и А2, А3 и А4 независимые, то
Р(А1А2) = Р(А1)Р(А2) и Р(А3А4) = Р(А3)P(А4).
Найдём вероятности событий А1, А2, А3, А4:
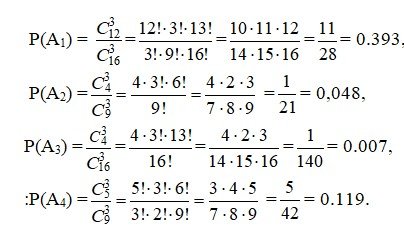
Получаем Р(А1А2) = = 0,441...
Потяни
